Gerhard Zugmaier^{1 *}, Franco Locatelli²

¹Department of Hematology, Oncology and Immunology, Philipps University Marburg, Marburg, Germany
²Department of Pediatrics, Sapienza, University of Rome, Director Department of Pediatric Hematology and Oncology IRCCS Ospedale Pediatrico Bambino Gesù, Rome, Italy

*Corresponding Author: Gerhard Zugmaier, Department of Hematology, Oncology and Immunology, Philipps University Marburg, Marburg, Germany.

Abstract
The characterization of acute leukemias has made tremendous progress in the last 10 years. It is now possible to detect acute leukemias at an early stage of bone marrow involvement, which is important for monitoring the treatment success for this disease. Leukemic cells can be discriminated from normal bone marrow cells through standardized and sophisticated methods. Risk stratification based also on the assessment of residual leukemia cells after initial weeks of therapy can assign patients to the appropriate treatment. This success has been made possible by adding modern technology such as immune phenotyping and molecular biology as diagnostic tools to conventional microscopy. While this progress in science has served patients, the right categorization of acute leukemias has become more complex for the treating physician. Numerous factors need to be determined to categorize the different types of acute leukemias for a tailored treatment approach defined by the risk of relapse and death from the disease. Mathematical logic is also known as Boolean algebra offers a useful tool to automatize the definition and diagnosis of acute leukemias. Boolean algebra is a sub-discipline of algebra, which in form of algebraic biology has become a major part of theoretical biology. Although the diseases can be correctly defined by verbal terms, mathematical logic in form of Boolean algebra may provide concise mathematical definitions. We defined the combination of findings by the truth values “1” or “0”.

Today the diagnosis of acute leukemia requires the microscope, immune phenotyping, and cytogenetic/molecular methods. These 3 factors are necessary and sufficient for the diagnosis of acute leukemias. However, this multifactor approach bears the risk of missing a factor for the correct diagnosis.

Boolean algebra (mathematical logic) may be able to minimize this risk by a mathematical definition of disease. The methods of mathematical logic were described previously [24,25]. We use mathematic logic as a form of algebra also called Boolean algebra. Boolean algebra is better characterized as a permutation of the truth values 1 and 0 than as “logic” in the traditional sense. Wittgenstein

[23] and the mathematician Emil Post [18] first described the permutations of the truth values 1 and 0 by truth tables. We will use Boolean algebra in this study in the same way as it is used in computer science [10].

Mathematical methods have been applied for diagnosis and definition of the disease since the beginning of the 20^th century [2, 6, 7, 9, 12, 13, 15]

Since we consider the term “Boolean algebra” better suited, we will use it synonymously with the term “Mathematical Logic”. In this study, we set out to describe the Definition of ALL and AML by Boolean algebra.

Methods
True items are coded by the number 1, false items by the number 0. An item can only have one value at a time, 1 for “true” and 0 for “false”. An item can stand for anything such as sentence, symptom, finding, or all together. The content has no relevance. The values of 2 items A and B can be listed by 4 permutations.

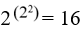
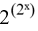
There are permutations possible for truth values of the item “AB” including the 2 combined items A and B. For x combined items the permutations of truth values would be . Through this approach, the permeations of truth values of all items can be coded by a sequence of the numbers 1 and 0 [24]. From the 16 possible permutations truth values of 2 combined items, the ones used in this study are listed below.

Permutation I

Verbal expression: Both A and B
Symbolic expression: A ∧ B

1 ∧ 1 = 1

1 ∧ 0 = 0

0 ∧ 1 = 0

0 ∧  0 = 0

Permutation II

Verbal expression: At least one A or B
Symbolic expression: A V B

This operator was introduced by Jevons in 1864 [3]. By doing this, Jevons created today’s Boolean algebra, which differs from the one, Boolean had created.

1 v 1 = 1

1 v 0 = 1

0 v 1 = 1

0 v 0 = 1

Permutation III

Verbal expression: If and only if A then B, or if A then B and vice versa Symbolic expression: A ↔ B

1 ↔ 1 = 1

1 ↔ 0 = 0

0 ↔ 1 = 0

0 ↔ 0 = 1

The algebra is defined as follows:

In the formulas, brackets “()” take precedence over each symbol, “∧” takes precedence over “v”, the latter takes precedence over each one of

“→” and “↔” [21].

Distributivity of “v” over “∧”: (A v B) ∧ (C v D) = A ∧ C v A ∧ D v B ∧ C v B ∧ D

Symbolic expression for “not”: ┐

┐1 = 0

┐0 = 1

De Morgan’s laws: ┐ (A ∧ B) = ┐A v ┐B; ┐(A v B) = ┐A ∧ ┐B

Unfortunately, the notation of Boolean algebra is not unified, even the arithmetic symbols + for v and x for ∧ are used. The arithmetic symbol + is also used for “either-or but not both” To avoid this ambiguity, in computer science the terms AND instead of ∧ and OR instead of v are used, ┐A ∧ ┐B is expressed as A NOR B, ┐ (A ∧ B) is expressed as A NAND B, “either A or B but not both” is expressed as A XOR B (Table 1). Computer chips are designed by only use of NAND or NOR. Boolean algebras can be defined in multiple ways and are introduced in different ways in the literature [10].

Table 1: Summary of Boolean Operators

The symbol "∈" from set theory is used, if at least 1 element is included in a set (Halbach 2010). 

Abbreviations
N nucleus, C cytoplasm AML Acute Myeloid Leukemia, ALL Acute Lymphoblastic Leukemia, CD Clustered designation (differentiation), M Myeloid, MDS Myelodysplastic Syndrome, MPAL Mixed phenotype acute leukemia, MPO Myeloperoxidase, MRC Myelodysplasia-related changes, NK Natural Killer, NOS Not otherwise specified, TdT terminal deoxynucleotidyl transferase consistently.

Results

1.0 Precursor lymphoid neoplasms ↔ B-lymphoblastic leukemia/lymphoma NOS v B-lymphoblastic leukemia/lymphoma with recurrent genetic abnormalities v T- lymphoblastic leukemia/lymphoma v NK- lymphoblastic leukemia/lymphoma

Synonyms: Pro-B lymphoblastic leukemia; common precursor B-lymphoblastic leukemia; pre- B lymphoblastic leukemia; common lymphoblastic leukemia; precursor-cell lymphoblastic lymphoma; precursor B-cell lymphoblastic leukemia; B-cell acute lymphoblastic leukemia

1.1 B-lymphoblastic leukemia NOS B-lymphoblastic leukemia/lymphoma NOS ↔ (CD19 strong v CD10 strong) ∧ (CD22 strong v CD79a strong) ∧ (CD45 strong v CD45 weak v CD38 strong v CD38 weak v CD58 strong v CD58 weak v TdT). Details are described elsewhere (Zugmaier and Locatelli 2020)

1.2 B-lymphoblastic leukemia/lymphoma with recurrent genetic abnormalities ↔ t (9;22) V KMT2A (MLL) rearrangement v t (12;21) v ((hyper diploid v hypodiploid) ∧ CD19 – positive v CD10 – positive)) V t (5;14) V t(1;19) V t  (17;19) v Ph-like v iAMP21. Details and risk stratification are described elsewhere (Zugmaier and Locatelli 2021)

1.3 T-lymphoblastic leukemia/lymphoma ↔ CD3 ∧ (TdT v CD1a v CD2 v CD3 v CD4 v CD6 v CD7 v CD8 v CD34 v CD99) Synonyms: Precursor T-lymphoblastic leukaemia/lymphoma; T ALL

1.4 NK-lymphoblastic
leukemia/lymphoma ↔ CD94-1A transcripts v CD56 ∧ CD7 ∧ CD2 NK is a provisional entity, and more research is warranted to define it more accurately.

2.0 Acute myeloid leukemia (AML) and related precursor neoplasms ↔ AML ∧ recurrent genetic abnormalities v AML ∧ MRC changes v therapy-related myeloid neoplasms v AML NOS v myeloid sarcoma v myeloid proliferations ∧ Down Syndrome

2.1 AML ∧ recurrent genetic abnormalities ↔ 1=t(8;21) v 2=inv(16) v 3=t(16;16) v 4=PML-RARA v 5=t(9;11) v 6=t(6;9) v 7=inv(3) v 8=t(3;3) v 9=t(1;22) v 10=BCR-ABL1 v 11=mutated NPM1 v 12=mutated CEPRA v 13=mutated RUNX1

2.1.1 Increased Risk of Relapse ↔ 6 v 7 v 8 v 9 v 10 v 13

2.1.2 Decreased Risk of Relapse ↔ 1 v 2 v 3 v 4 v 11 v12

2.2 AML ∧ MRC ↔ blasts > 20% ∧ (prior MDS v MDS - related     genetic abnormalities v multilineage dysplasia) ∧ ┐(chemotherapy v radiotherapy v AML ∧ recurrent genetic abnormalities)

2.3 Therapy-related myeloid neoplasm ↔ alkylating agents v radiation therapy v topoisomerase II inhibitors v antimetabolites v anti tubulin agents

2.3.1 Alkylating agents ↔ melphalan v cyclophosphamide v nitrogen mustard v chlorambucil v busulfan v carboplatin v cisplatin v dacarbazine v procarbazine v carmustine v mitomycin C v thiotepa v iomustine

2.3.2 Topoisomerase II inhibitors ↔ etoposide v teniposide v doxorubicin or daunorubicin v mitoxantrone v amsacrine v actinomycin

2.3.3 Antimetabolites ↔ thiopurines v mycophenolate v mofetil v fludarabine

2.3.4 Antitubulin agents ↔ vincristine v vinblastine v vindesine v paclitaxel v docetaxel

2.4 AML NOS ↔ AML ∧ minimal differentiation v AML ∧ (┐maturation v maturation) v acute leukemia ∧ (myelomonocytic v monoblastic v monocytic) v pure erythroid leukemia v acute megakaryoblastic leukemia v acute basophilic/mast cell leukemia v acute panmyelosis ∧ myelofibrosis

2.4.1 AML ∧ minimal differentiation ↔ CD13 ∧ CD117

2.4.2  AML ∧ ┐maturation ↔ (MPO > 3% blasts v Sudan Black > 3% blasts) ∧ granulocyte lineage <10% v Auer rods ∧ (CD13 v CD 33 v CD117)

2.4.3 AML ∧ maturation ↔ blasts > 20 % ∧ granulocyte lineage > 10% ∧ monocyte lineage < 20% ∧ (CD13 v CD33 v CD65 v CD11b v CD15)

2.4.4  Acute myelomonocytic leukemia ↔ blasts > 20% ∧ granulocyte lineage > 20 % ∧ monocyte lineage > 20 % ∧ (CD13 v CD33 v CD65 v CD15)

2.4.5 Acute leukemia ∧ (monoblastic v monocytic) ↔ blasts > 20 % ∧ monocytic lineage cells > 80 % ∧ neutrophils < 20 % ∧ (CD13 v CCD33 v CD65 v CD15)

2.4.6 Erythroid leukemia ↔ erythroid lineage > 80 % ∧ proerythroblasts > 30 %)

2.4.7 Acute megakaryoblast leukemia ↔ blasts > 20 % ∧ megakaryocyte linage > 50 %)

2.4.8 Acute panmyelosis ∧ myelofibrosis ↔ blasts > 20 % ∧ fibrosis of bone marrow.

2.4.9 Acute basophilic leukemia ↔ Toloudine Blue ∧ high N:C ratio ∧ dispersed chromatin ∧ ┐ (CD117 v CD25) ∧ (CD13 v CD33 v CD123 v CD203C v CD11b)

2.4.9.1 Mast cell leukemia ↔ CD117 ∧ Mast Cell Tryptase ∧ CD25 

2.5  Myeloid sarcoma ↔ myeloid blasts ∧ ┐AML bone marrow

2.6 Myeloid proliferation and Down Syndrome ↔ Down Syndrome ∧ (transient abnormal megakaryoblastic myeloporesis v acute megakaryoblastic leukemia)

2.7  Blastic plasmacytoid dendritic cell neoplasm ↔ CD4 ∧ CD56 ∧ CD68 ∧ CD123 ∧ TCL1A ∧ CD303 ∧ BCL11A

3. Lineages

3.1. Myeloid lineage ↔ MPO v (Monocytic ↔ >2 € {non-specific esterase; CD11c; CD14; CD64; lysozyme})

3.2. T-cell lineage ↔ CD3

3.3. B-cell lineage ↔ (CD19 v CD10) ∧ (CD22 v CD79a)

Acute leukemia of ambiguous origin ↔ acute undifferentiated leukemia v MPAL

4.1. Acute undifferentiated leukemia ↔ ┐(myeloid lineage v T- cell lineage v B-cell lineage)

4.2. MPAL ↔ myeloid lineage ∧ (B-cell lineage v T-cell lineage)

Discussion
In this study, we have described Boolean algebra as a mathematical tool for the definition of complicated diseases such as acute leukemias.

While theoretical physics, theoretical chemistry and theoretical biology were established as academic disciplines in the 20^th century, theoretical medicine remains to be developed. The application of many different disciplines such as mathematics, physics, computer science, chemistry, biology, and law may have been an obstacle to building a uniform theoretical basis of medicine as done for other disciplines [14].

The implementation of discrete mathematics into biology in the last 20 years has exerted a major influence on theoretical biology, which had before been mainly driven by continuous models with differential equations derived from analysis like in theoretical physics and theoretical chemistry. Discrete mathematics is more suited for models in biology than the continuous tools of analysis. Boolean algebra, a subdiscipline of discrete mathematics and algebra, has found multiple applications in biology, such as in gene regulatory networks or signaling networks [1].

Boolean models have been used to predict clinical outcomes from somatic mutations in AML [15]. This study is one of the 1^st concrete approaches to use Boolean methods for the definition of disease. Although disease can easily be defined in verbal terms, the multifactorial definition based on multiple genetic and immunologic markers makes a mathematical approach more suitable [8]. Acute leukemias with their many strata to define multiple entities give a prime example for the complicated diagnostic process as a prerequisite for patient-tailored treatment. However, it goes without saying that Boolean algebra cannot substitute for a thorough understanding of pathophysiology and the patient-physician interaction. A mathematical system will never be able to cover medicine completely because of improving and thereby changing concepts of disease [7]. Therefore, the mathematical system used in this study does not have the purpose to describe the nature of the disease or pathophysiologic mechanisms. Mathematical methods will never replace the physician but can relieve the busy clinician from mechanical tasks, which may prevent her or him from interacting with the patient. However, in the end, physicians will always have the obligation to assess mathematical models in the context of clinical reality.

References

1. Albert R, Robeva R (2015) Signaling Networks: Asynchronous Boolean Models, in: ALGEBRAIC AND DISCRETE MATHEMTICAL MODELS FOR BIOLOGY.
2. Bieganski W (1909) Medizinische Logik, Kritik der ärztlichen Erkenntnis. Fabian A., Kabitzsch, Würzburg.
3. Brown FM (2003) BOOLEAN REASONING, The Logic of Boolean Equations, second edition, Dover Publications, Mineola, New York.
4. Cohen H (1943) The nature of methods and purpose of diagnosis, Lancet I. 241(6227): 23-25
5. Faderl, Stefan H, Kantarjian, Hagop M, Estey, et al. (2021) Acute leukemias, second edition, Springer.
6. Gross R (1969) Medizinische Diagnostik-Grundlagen und Praxis. Springer Verlag, Berlin, Heidelberg, New York.
7. Gross, Rudolf, Löffler, Markus (1997) Prinzipien der Medizin, Springer, Heidelberg.
8. Halbach V (2010) The Logic Manual. Oxford University Press, Oxford.
9. He Q, Macaualey M, Davies R (2015) Dynamics of Boolean Networks: Canalization, Stability, and Criticality, in: Algebraic and discrete mathemtical models for biology. 93-119
10. Hoffmann DW (2016) GRUNDLAGEN DER TECHNISCHEN INFOMATIK, 5. Auflage Carl Hanser Verlag München. 1-10.
11. Iacobucci I, Mulligan CG (2017) Genetic Basis of Acute Lymphoblastic Leukemia, Journal of Clinical Oncology. 35(9): 975-983
12. Lin, Kent PC, Khatri, Sunil P (2014) Logic Synthesis for Genetic Diseases. Modeling Disease Behavior Using Boolean Networks, Springer, New York, Heidelberg, Dodrecht, London.
13. Mainzer F, Über die logischen Prinzipien der ärztlichen Diagnose in Schaxel J., Abhandlungen zur Theoretischen Biologie, Gebrüder Bornträger, Berlin 1925
14. Matthäus F, Matthäus S, Harris SA, Hillen T (2020) The Art of Theoretical biology, Springer.
15. Palma A, Iannuccelli M, Rozzo I, Licata L, Perfetto L, et al. (2021) Integrating Patient-Specific Information into Logic Models of Complex Diseases: Application to Acute Myeloid Leukemia. J Pers Med. 11(2): 117.
16. Peano G (1889) The prinicples of arithmetic presented by a new method.
17. Heijencourt JV (1967) From Frege to Gödel: a source book in mathematical logic, 1879-1931. Harvard University Press, Cambridge, London.
18. Post E. 1921, Introduction to a general theory of elementary proposition in Heijencourt J., From Frege to Gödel, Harvard University Press, Cambridge, London 1967
19. Robeva RS (2015) ALGEBRAIC AND DISCRETE MATHEMTICAL MODELS FOR BIOLOGY, edited by, Elsevier, Amsterdam, Boston, London, New York, Oxford, Paris, San Diego, San Francisco, Singapore, Sidney, Tokyo.
20. Swedlow SH, Campo E, Harris NL, Jaffe ES, Pileri SA, et al. (2017) WHO Classification of Tumours of Haematopoietic and Lymphoid Tissues, 4^th Edition, IARC, Lyon.
21. Takeuti G (1987) Proof Theory. 2^nd Edition, Dover Publications, Mineola, New York.
22. Thiel C (1965) Sinn und Bedeutung in der Logik Gottlob Freges. Philosophische Forschung, Monographie 43, A. Hain, Meisenheim.
23. Wittgenstein L (1992) Tractatus logico-philosophicus, Suhrkamp, Berlin.
24. Zugmaier G, Locatelli F (2020) Application of Mathematical Logic for immunophenotyping of B-Cell precursor acute lymphoblastic leukemia (BCP-ALL). Biomed Genet Genomics. 4: 1-3.
25. Zugmaier G, Locatelli F (2021) Application of Mathematical Logic for Cytogenetic Definition and Risk Stratification of B- Cell Precursor Acute Lymphoblastic Leukemia (BCP-ALL) Medical Research Archives 9(2): 1-8.